1 Welcome to the heat sink computation toolbox

Heat sink dimensioning based on analytical calculation of thermal resistance.

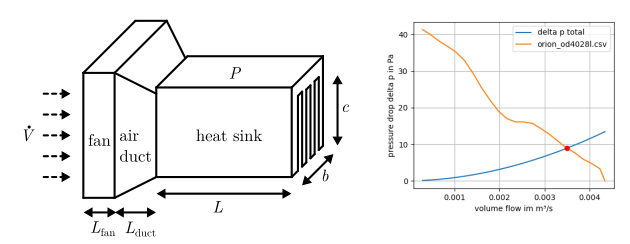
The pressure loss through the cooling system is determined by the specified geometry and the fan. This allows the volume flow rate to be determined. The volume flow can then be used to determine the thermal resistance.

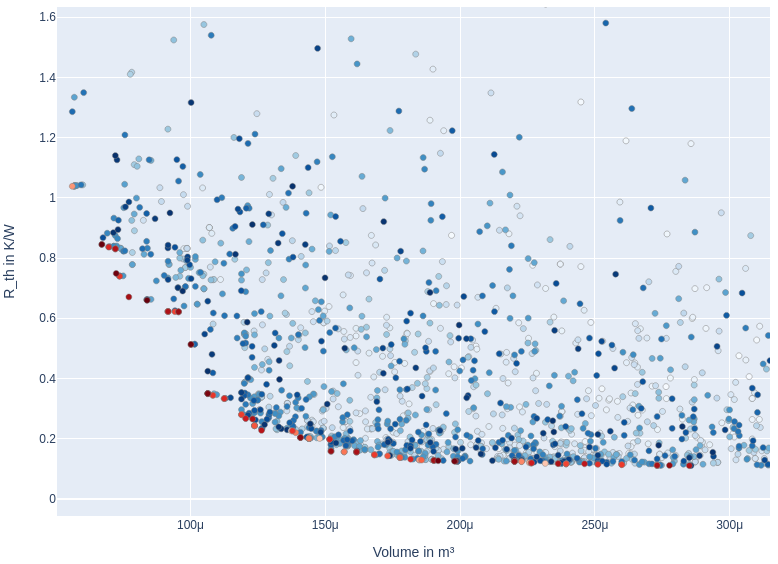
The estimate of the geometry parameters and the fan is mapped to the costs (volume, R_th) using Pareto optimization. About 40 fan characteristic curves are stored in the toolbox.

1.1 Installation

Install in developer mode.

git clone git@github.com:upb-lea/HCT_heat_sink_computation_toolbox.git cd HCT_heat_sink_computation_toolbox/ pip install -e .

1.2 Usage and examples

Check out the examples in this directory.

1.3 Literature

This toolbox implements the thermal basics according to the following paper:

Christoph Gammeter, Florian Krismer and Johann W. Kolar Weight Optimization of a Cooling System Composed of Fan and Extruded Fin Heat Sink

Heat spreading is implemented according to the following Ph.D. thesis:

Christoph Gammeter Multi-Objective Optimization of Power Electronics and Generators of Airborne Wind Turbines

This is supplemented by various calculations and optimizations. E.g. a Pareto optimization is added.

1.4 Bug reports

Please use the issues report button within GitHub to report bugs.

1.5 Contributing

Pull requests are welcome. For major changes, please open an issue first to discuss what you would like to change.

1.6 Changelog

Find the changelog here.

2 Heat Sink Computation Toolbox (HCT) Function Documentation

Plot settings: Normal font or LaTeX font.

hct.generalplotsettings.colors() → dict

Colors according to the GNOME color scheme (Color 4).

hct.generalplotsettings.global_plot_settings_font_latex() → None

Set the plot fonts to LaTeX-font.

hct.generalplotsettings.global_plot_settings_font_sansserif() → None

Set the plot fonts to Sans-Serif-Font.

hct.generalplotsettings.global_plot_settings_font_size(font_size: float) → None

Change the plot font size.

Parameters:

font_size (float) – font size

Heat spreading calculation according to doctor thesis.

Christoph Gammeter Multi-Objective Optimization of Power Electronics and Generators of Airborne Wind Turbines

hct.heat_spreading.calc_biot_number(heat_spreading_material: SpreadingMaterial, r_th_zero: float) → float

Calculate the biot number.

Parameters:

• heat_spreading_material – heat spreading material

• r_th_zero – thermal resistance for the rest of the system (cooling fins)

hct.heat_spreading.calc_dimensionless_constriction_resistance_psi(epsilon_spreading_material: float, phi_c: float) → float

Calculate the dimensionless constriction resistance.

Parameters:

• epsilon_spreading_material – dimensionless geometry factor of the heat sink

• phi_c – phi_c according to paper

hct.heat_spreading.calc_epsilon_spreading_material(heat_spreading_material: SpreadingMaterial) → float

Calculate the dimensional factor for the heat spreading material.

Parameters:

heat_spreading_material – SpreadingMaterial

hct.heat_spreading.calc_phi_c(tau: float, sigma_c: float, biot_number: float) → float

Calculate phi_c.

Parameters:

• tau – tau

• sigma_c – sigma_c

• biot_number – biot number

hct.heat_spreading.calc_r_th_m(heat_spreading_material: SpreadingMaterial) → float

Calculate the R_th,d (heat sink, baseplate).

Parameters:

heat_spreading_material (SpreadingMaterial) – heat spreading material according to SpreadingMaterial class

Returns:

r_th_d in K/W

hct.heat_spreading.calc_r_th_sp(spreading_material: SpreadingMaterial, r_th_zero: float) → float

Calculate the r_th_sp for the spreading material.

Parameters:

• spreading_material – SpreadingMaterial

• r_th_zero – r_th_zero, according to the paper, the rest of the heat sink.

hct.heat_spreading.calc_sigma_c(epsilon_spreading_material: float) → float

Calculate the sigma_c factor.

Parameters:

epsilon_spreading_material – Epsilon for the spreading material

hct.heat_spreading.calc_spreading_resistance_r_f(heat_spreading_material: SpreadingMaterial, psi: float)

Calculate the spreading resistance r_f.

Parameters:

• psi – dimensionless constriction resistance

• heat_spreading_material – SpreadingMaterial

hct.heat_spreading.calc_tau(heat_spreading_material: SpreadingMaterial) → float

Calculate the tau factor.

Parameters:

heat_spreading_material – SpreadingMaterial

hct.heat_spreading.verify_with_phd_thesis_gammeter() → None

Verify with figure 3.18 (page 149), Ph.D. thesis Gammeter.

Implementation of the hydrodynamic model according to a given paper.

Christoph Gammeter, Florian Krismer, Johann Kolar: ‘Weight Optimization of a Cooling System Composed of Fan and Extruded Fin Heat Sink’

hct.hydrodynamic.calc_delta_p_acc(geometry: Geometry, volume_flow_v_dot: float, constants: Constants)

Calculate the pressure drop for the frictionless fluid flow acceleration.

Parameters:

• geometry – geometry of the heat sink

• volume_flow_v_dot – volume flow in m³/s

• constants – constants

Returns:

pressure drop in Pascal (Pa)

hct.hydrodynamic.calc_delta_p_duct(f_app_duct: float, l_duct: float, mean_d_h_duct: float, constants: Constants, mean_u_duct: float)

Calculate the duct static pressure drop.

Parameters:

• f_app_duct (float) – apparent friction factor for viscous fluid flow in the air duct

• l_duct (float) – length of the air duct

• mean_u_duct (float) – average velocity inside the heat sink

• mean_d_h_duct (float) – average velocity inside the air duct

• constants (Constants) – constants according to the Constants class

Returns:

pressure difference of the air duct in Pascal (Pa)

hct.hydrodynamic.calc_delta_p_heat_sink(f_app: float, k_se: float, k_sc: float, constants: Constants, geometry: Geometry, d_h: float, mean_u_hs: float) → float

Calculate the pressure drop of the heat sink.

Parameters:

• f_app (float) – apparent friction factor for viscous fluid flow in ducts

• k_se (float) – friction factor for sudden contraction

• k_sc (float) – friction factor for sudden expansion

• constants (Constants) – Constants.

• geometry (Geometry) – Geometry.

• d_h (float)

• mean_u_hs (float) – average velocity inside the heat sink

Returns:

delta_p_heat_sink in Pascal (Pa).

Return type:

float

hct.hydrodynamic.calc_epsilon_duct(geometry: Geometry)

Calculate the epsilon shape factor from the air duct geometry.

Parameters:

geometry – Geometry parameters

Returns:

Epsilon shape factor for the air duct.

hct.hydrodynamic.calc_f_app(geometry: Geometry, constants: Constants, volume_flow_v_dot: float, f_re_sqrt_a: float)

Calculate the apparent friction factor for the average duct hydraulic parameter.

Parameters:

• geometry – Geometry.

• constants – Constants.

• volume_flow_v_dot – volume flow in m³/s

• f_re_sqrt_a

Returns:

Apparent friction factor for the average duct hydraulic parameter.

hct.hydrodynamic.calc_f_app_duct(constants: Constants, geometry: Geometry, volume_flow_v_dot: float, f_re_sqrt_a_fd: float)

Calculate the apparent friction factor for the average duct hydraulic diameter.

Parameters:

• constants (Constants) – Constants

• geometry (Geometry) – Geometry

• volume_flow_v_dot (float) – Volume flow in m³/s

• f_re_sqrt_a_fd (float) – f_re_sqrt_a_fd

Returns:

Apparent friction factor for the average duct hydraulic diameter.

hct.hydrodynamic.calc_k_sc(geometry: Geometry)

Calculate the friction factor sudden expansion.

Parameters:

geometry – Geometry.

Returns:

Friction factor sudden expansion.

hct.hydrodynamic.calc_k_se(geometry: Geometry)

Calculate the friction factor for sudden contraction.

Parameters:

geometry – Geometry

Returns:

friction factor for sudden contraction.

hct.hydrodynamic.calc_l_duct(geometry: Geometry)

Calculate the length of the air duct.

Parameters:

geometry – Geometry

Returns:

Length of the air duct.

hct.hydrodynamic.calc_mean_d_h_duct(geometry: Geometry)

Calculate the mean average velocity inside the air duct.

Parameters:

geometry – Geometry

Returns:

mean average velocity inside the air duct.

hct.hydrodynamic.calc_mean_u_duct(geometry: Geometry, volume_flow_v_dot: float)

Calculate the average velocity inside the air duct.

Parameters:

• geometry – Geometry of the heat sink

• volume_flow_v_dot – volume flow in m³/s

Returns:

average velocity inside the air duct in m/s.

hct.hydrodynamic.calc_mean_u_hs(geometry: Geometry, volume_flow_v_dot: float)

Calculate the average velocity inside the heat sink.

Parameters:

• geometry – Geometry of the heat sink

• volume_flow_v_dot – volume flow in m³/s

Returns:

average velocity inside the heat sink in m/s.

hct.hydrodynamic.calc_volume_flow(fan_name: str, geometry: Geometry, plot: bool = False, figure_size: tuple | None = None)

Calculate the volume flow for a given fan and a given geometry.

This function calculates the intersection of both graphs, the fan graph and the heat sink pressure graph and returns the intersection point.

Parameters:

• fan_name (str) – file name including .csv ending

• geometry (Geometry) – Geometry.

• plot (bool) – True to show a visual output.

• figure_size (tuple) – Figure size in mm, e.g. (80, 60) is a 80 mm wide and 60 mm height plot

Returns:

intersection_volume_flow, intersection_pressure

hct.hydrodynamic.calculate_intersection(x_list: ndarray, y1_list: ndarray, y2_list: ndarray) → ndarray

Calculate the intersection between two graphs (x_list, y1_list) and (x_list, y2_list).

The return are both lists (x_list, y1_list) and (x_list, y2_list) added by the intersection points as well as the intersection point itself. :param x_list: common x-coordinates of the two graphs :type x_list: np.ndarray :param y1_list: y-coordinates of graph 1 :type y1_list: np.ndarray :param y2_list: y-coordinates of graph 2 :type y2_list: np.ndarray :return: x_list, y1_list, y2_list (lists are complemented by the intersection point), x_intersection, y_intersection

hct.hydrodynamic.compare_fan_data() → None

Plot all available fan data for comparison.

hct.hydrodynamic.read_fan_data(filepath: str)

Read stored .csv fan data, translate curves with SI-unit outputs.

Parameters:

filepath – Filepath to fan .csv-file.

Returns:

fan_cubic_meter_second, fan_pressure_drop_pascal

Heat sink system optimization using optuna.

class hct.optimization.Optimization

Optuna optimization for heat sink and fan optimization.

static df_plot_pareto_front(df: DataFrame, figure_size: tuple) → None

Plot an interactive Pareto diagram (losses vs. volume) to select the transformers to re-simulate.

Parameters:

• df (pd.DataFrame) – DataFrame, generated from an optuna study (exported by optuna)

• figure_size (tuple) – figures size as a x/y-tuple in mm, e.g. (160, 80)

static load_config(config_pickle_filepath: str) → OptimizationParameters

Load pickle configuration file from disk.

Parameters:

config_pickle_filepath (str) – filepath to the pickle configuration file

Returns:

Configuration file as OptimizationParameters object

Return type:

OptimizationParameters

static objective(trial: Trial, config: OptimizationParameters) → tuple

Objective for the optimization with optuna.

Parameters:

• trial (optuna.Trial) – optuna input suggestions

• config (OptimizationParameters) – optimization configuration according to OptimizationParameters class

Returns:

total_volume, r_th_sa in case of success, nan,nan in case of unrealistic geometry parameters

static save_config(config: OptimizationParameters) → None

Save the configuration file as pickle file on the disk.

Parameters:

config (OptimizationParameters) – configuration

static start_proceed_study(config: ~hct.thermal_dataclasses.OptimizationParameters, number_trials: int, storage: str = 'sqlite', sampler: ~optuna.samplers._base.BaseSampler = <optuna.samplers._nsgaiii._sampler.NSGAIIISampler object>) → None

Proceed a study which is stored as sqlite database.

Parameters:

• number_trials (int) – Number of trials adding to the existing study

• storage (str) – storage database, e.g. ‘sqlite’ or ‘mysql’

• sampler (optuna.sampler-object) – optuna.samplers.NSGAIISampler() or optuna.samplers.NSGAIIISampler(). Note about the brackets () !! Default: NSGAIII

• config (OptimizationParameters) – configuration according to OptimizationParameters class

static study_to_df(config: OptimizationParameters) → DataFrame

Create a Pandas DataFrame from a study.

Parameters:

config (OptimizationParameters) – configuration

Returns:

Study results as Pandas DataFrame

Return type:

pd.DataFrame

Data class definitions.

class hct.thermal_dataclasses.Constants(c_1: float, c_2: float, c_3: float, c_4: float, gamma: float, rho_air: float, c_air: float, lambda_air: float, fluid_viscosity_air: float, lambda_material: float, rho_material: float, k_venturi: float)

Define constants.

class hct.thermal_dataclasses.FanData(manufacturer: str, type: str, width_height: float, length: float, weight: float, datasheet: str)

Define fan data.

class hct.thermal_dataclasses.Geometry(height_c: float, width_b: float, length_l: float, height_d: float, number_fins_n: int, thickness_fin_t: float, fin_distance_s: float, alpha_rad: float, l_duct_min: float)

Define a single heat sink geometry.

l_duct_min: minimum length of the air duct.

class hct.thermal_dataclasses.OptimizationParameters(heat_sink_study_name: str, heat_sink_optimization_directory: str, height_c_list: List, width_b_list: List, length_l_list: List, height_d_list: List, number_fins_n_list: List, thickness_fin_t_list: List, fan_list: List, t_ambient: float, number_directions: int, area_min: float | None)

Define optimization parameters.

2 directions: Optimize for minimum volume and minimum R_th, 3 directions: Optimize for minimum volume, minimum R_th and minimum surface area A_min.

class hct.thermal_dataclasses.SpreadingMaterial(lambda_conductivity: float, thickness_d: float, heat_source_area_a_s: float, spreading_material_area_a_sp: float)

Define the heat spreading material.