Electric Motors

Electric Motor Base Class

class gym_electric_motor.physical_systems.electric_motors.ElectricMotor(motor_parameter=None, nominal_values=None, limit_values=None, motor_initializer=None, initial_limits=None)[source]

Base class for all technical electrical motor models.

A motor consists of the ode-state. These are the dynamic quantities of its ODE. For example:

ODE-State of a DC-shunt motor: `` [i_a, i_e ] ``

  • i_a: Anchor circuit current

  • i_e: Exciting circuit current

Each electric motor can be parametrized by a dictionary of motor parameters, the nominal state dictionary and the limit dictionary.

Initialization is given by initializer(dict). It can be constant state value or random value in given interval. dict should be like: { ‘states’(dict): with state names and initital values

‘interval’(array like): boundaries for each state

(only for random init), shape(num states, 2)

‘random_init’(str): ‘uniform’ or ‘normal’ ‘random_params(tuple): mue(float), sigma(int)

Example initializer(dict) for constant initialization:

{ ‘states’: {‘omega’: 16.0}}

Example initializer(dict) for random initialization:

{ ‘random_init’: ‘normal’}

Parameters:

  • motor_parameter – Motor parameter dictionary. Contents specified for each motor.

  • nominal_values – Nominal values for the motor quantities.

  • limit_values – Limits for the motor quantities.

  • motor_initializer –

    Initial motor states (currents) (‘constant’, ‘uniform’, ‘gaussian’ sampled from

    given interval or out of nominal motor values)

  • initial_limits – limits for of the initial state-value

CURRENTS = []

List of the motor currents names

Type:

CURRENTS(list(str))

CURRENTS_IDX = []

Indices for accessing all motor currents.

Type:

CURRENTS_IDX(list(int))

HAS_JACOBIAN = False

Parameter indicating if the class is implementing the optional jacobian function

VOLTAGES = []

List of the motor input voltages names

Type:

VOLTAGES(list(str))

electrical_jacobian(state, u_in, omega, *_)[source]

Calculation of the jacobian of each motor ODE for the given inputs / The motors ODE-System.

Overriding this method is optional for each subclass. If it is overridden, the parameter HAS_JACOBIAN must also be set to True. Otherwise, the jacobian will not be called.

Parameters:

  • state (ndarray(float)) – The motors state.

  • u_in (list(float)) – The motors input voltages.

  • omega (float) – Angular velocity of the motor

Returns:

[0]: Derivatives of all electrical motor states over all electrical motor states shape:(states x states) [1]: Derivatives of all electrical motor states over omega shape:(states,) [2]: Derivative of Torque over all motor states shape:(states,)

Return type:

Tuple(ndarray, ndarray, ndarray)

electrical_ode(state, u_in, omega, *_)[source]

Calculation of the derivatives of each motor state variable for the given inputs / The motors ODE-System.

Parameters:

  • state (ndarray(float)) – The motors state.

  • u_in (list(float)) – The motors input voltages.

  • omega (float) – Angular velocity of the motor

Returns:

Derivatives of the motors ODE-system for the given inputs.

Return type:

ndarray(float)

i_in(state)[source]
Parameters:

state (ndarray(float)) – ODE state of the motor

Returns:

List of all currents flowing into the motor.

Return type:

list(float)

property initial_limits

Returns: dict: nominal motor limits for choosing initial values

initialize(state_space, state_positions, **__)[source]

Initializes given state values. Values can be given as a constant or sampled random out of a statistical distribution. Initial value is in range of the nominal values or a given interval. Values are written in initial_states attribute

Parameters:

  • state_space (gymnasium.Box) – normalized state space boundaries (given by physical system)

  • state_positions (dict) – indices of system states (given by physical system)

property initializer

Returns: dict: Motor initial state and additional initializer parameter

property limits

Readonly motors limit state array. Entries are set to the maximum physical possible values in case of unspecified limits.

Returns:

Limits of the motor.

Return type:

dict(float)

property motor_parameter

Returns: dict(float): The motors parameter dictionary

property nominal_values

Readonly motors nominal values.

Returns:

Current nominal values of the motor.

Return type:

dict(float)

reset(state_space, state_positions, **__)[source]

Reset the motors state to a new initial state. (Default 0)

Parameters:

  • state_space (gymnasium.Box) – normalized state space boundaries

  • state_positions (dict) – indexes of system states

Returns:

The initial motor states.

Return type:

numpy.ndarray(float)

Synchronous Motors

Parameter Dictionary

Key

Description

Default

r_s

Stator Resistance in Ohm

4.9

l_d

d-axis inductance in Henry

79e-3

l_q

q-axis inductance in Henry

113e-3

j_rotor

Moment of inertia of the rotor

2.45e-3

psi_p

Permanent linked rotor flux

0.165

p

Pole pair Number

2

All nominal voltages and currents are peak phase values. Therefore, data sheet values for line voltages and phase currents has to be transformed such that \(U_N=\sqrt(2/3) U_L\) and \(I_N=\sqrt(2) I_S\).

Furthermore, the angular velocity is the electrical one and not the mechanical one \(\omega = p \omega_{me}\).

class gym_electric_motor.physical_systems.electric_motors.SynchronousMotor(motor_parameter=None, nominal_values=None, limit_values=None, motor_initializer=None)[source]

The SynchronousMotor and its subclasses implement the technical system of a three phase synchronous motor.

This includes the system equations, the motor parameters of the equivalent circuit diagram, as well as limits and bandwidth.

Motor Parameter

Unit

Default Value

Description

r_s

Ohm

0.78

Stator resistance

l_d

H

1.2

Direct axis inductance

l_q

H

6.3e-3

Quadrature axis inductance

psi_p

Wb

0.0094

Effective excitation flux (PMSM only)

p

1

2

Pole pair number

j_rotor

kg/m^2

0.017

Moment of inertia of the rotor

Motor Currents

Unit

Description

i_sd

A

Direct axis current

i_sq

A

Quadrature axis current

i_a

A

Current through line a

i_b

A

Current through line b

i_c

A

Current through line c

i_alpha

A

Current in alpha axis

i_beta

A

Current in beta axis

Motor Voltages

Unit

Description

u_sd

V

Direct axis voltage

u_sq

V

Quadrature axis voltage

u_a

V

Phase voltage for line a

u_b

V

Phase voltage for line b

u_c

V

Phase voltage for line c

u_alpha

V

Phase voltage in alpha axis

u_beta

V

Phase voltage in beta axis

Limits /

Nominal Value Dictionary Entries:

Entry

Description

i

General current limit / nominal value

i_a

Current in phase a

i_b

Current in phase b

i_c

Current in phase c

i_alpha

Current in alpha axis

i_beta

Current in beta axis

i_sd

Current in direct axis

i_sq

Current in quadrature axis

omega

Mechanical angular Velocity

torque

Motor generated torque

epsilon

Electrical rotational angle

u_a

Phase voltage in phase a

u_b

Phase voltage in phase b

u_c

Phase voltage in phase c

u_alpha

Phase voltage in alpha axis

u_beta

Phase voltage in beta axis

u_sd

Phase voltage in direct axis

u_sq

Phase voltage in quadrature axis

Note

The voltage limits should be the peak-to-peak value of the phase voltage (\(\hat{u}_S\)). A phase voltage denotes the potential difference from a line to the neutral point in contrast to the line voltage between two lines. Typically the root mean square (RMS) value for the line voltage (\(U_L\)) is given as \(\hat{u}_S=\sqrt{2/3}~U_L\)

The current limits should be the peak-to-peak value of the phase current (\(\hat{i}_S\)). Typically the RMS value for the phase current (\(I_S\)) is given as \(\hat{i}_S = \sqrt{2}~I_S\)

If not specified, nominal values are equal to their corresponding limit values. Furthermore, if specific limits/nominal values (e.g. i_a) are not specified they are inferred from the general limits/nominal values (e.g. i)

Parameters:

  • motor_parameter – Motor parameter dictionary. Contents specified for each motor.

  • nominal_values – Nominal values for the motor quantities.

  • limit_values – Limits for the motor quantities.

  • motor_initializer –

    Initial motor states (currents) (‘constant’, ‘uniform’, ‘gaussian’ sampled from

    given interval or out of nominal motor values)

  • initial_limits – limits for of the initial state-value

CURRENTS = ['i_sd', 'i_sq']

List of the motor currents names

Type:

CURRENTS(list(str))

CURRENTS_IDX = [0, 1]

Indices for accessing all motor currents.

Type:

CURRENTS_IDX(list(int))

VOLTAGES = ['u_sd', 'u_sq']

List of the motor input voltages names

Type:

VOLTAGES(list(str))

electrical_ode(state, u_dq, omega, *_)[source]

The differential equation of the Synchronous Motor.

Parameters:

  • state – The current state of the motor. [i_sd, i_sq, epsilon]

  • omega – The mechanical load

  • u_qd – The input voltages [u_sd, u_sq]

Returns:

The derivatives of the state vector d/dt([i_sd, i_sq, epsilon])

i_in(state)[source]
Parameters:

state (ndarray(float)) – ODE state of the motor

Returns:

List of all currents flowing into the motor.

Return type:

list(float)

property initializer

Returns: dict: Motor initial state and additional initializer parameter

property motor_parameter

Returns: dict(float): The motors parameter dictionary

reset(state_space, state_positions, **__)[source]

Reset the motors state to a new initial state. (Default 0)

Parameters:

  • state_space (gymnasium.Box) – normalized state space boundaries

  • state_positions (dict) – indexes of system states

Returns:

The initial motor states.

Return type:

numpy.ndarray(float)

Synchronous Reluctance Motor

class gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor(motor_parameter=None, nominal_values=None, limit_values=None, motor_initializer=None)[source]

Motor Parameter

Unit

Default Value

Description

r_s

Ohm

0.57

Stator resistance

l_d

H

10.1e-3

Direct axis inductance

l_q

H

4.1e-3

Quadrature axis inductance

p

1

4

Pole pair number

j_rotor

kg/m^2

0.8e-3

Moment of inertia of the rotor

Motor Currents

Unit

Description

i_sd

A

Direct axis current

i_sq

A

Quadrature axis current

i_a

A

Current through branch a

i_b

A

Current through branch b

i_c

A

Current through branch c

i_alpha

A

Current in alpha axis

i_beta

A

Current in beta axis

Motor Voltages

Unit

Description

u_sd

V

Direct axis voltage

u_sq

V

Quadrature axis voltage

u_a

V

Voltage through branch a

u_b

V

Voltage through branch b

u_c

V

Voltage through branch c

u_alpha

V

Voltage in alpha axis

u_beta

V

Voltage in beta axis

Limits /

Nominal Value Dictionary Entries:

Entry

Description

i

General current limit / nominal value

i_a

Current in phase a

i_b

Current in phase b

i_c

Current in phase c

i_alpha

Current in alpha axis

i_beta

Current in beta axis

i_sd

Current in direct axis

i_sq

Current in quadrature axis

omega

Mechanical angular Velocity

epsilon

Electrical rotational angle

torque

Motor generated torque

u_a

Voltage in phase a

u_b

Voltage in phase b

u_c

Voltage in phase c

u_alpha

Voltage in alpha axis

u_beta

Voltage in beta axis

u_sd

Voltage in direct axis

u_sq

Voltage in quadrature axis

Note: The voltage limits should be the peak-to-peak value of the phase voltage (\(\hat{u}_S\)). A phase voltage denotes the potential difference from a line to the neutral point in contrast to the line voltage between two lines. Typically the root mean square (RMS) value for the line voltage (\(U_L\)) is given as \(\hat{u}_S=\sqrt{2/3}~U_L\)

The current limits should be the peak-to-peak value of the phase current (\(\hat{i}_S\)). Typically the RMS value for the phase current (\(I_S\)) is given as \(\hat{i}_S = \sqrt{2}~I_S\)

If not specified, nominal values are equal to their corresponding limit values. Furthermore, if specific limits/nominal values (e.g. i_a) are not specified they are inferred from the general limits/nominal values (e.g. i)

Parameters:

  • motor_parameter – Motor parameter dictionary. Contents specified for each motor.

  • nominal_values – Nominal values for the motor quantities.

  • limit_values – Limits for the motor quantities.

  • motor_initializer –

    Initial motor states (currents) (‘constant’, ‘uniform’, ‘gaussian’ sampled from

    given interval or out of nominal motor values)

  • initial_limits – limits for of the initial state-value

HAS_JACOBIAN = True

Parameter indicating if the class is implementing the optional jacobian function

electrical_jacobian(state, u_in, omega, *_)[source]

Calculation of the jacobian of each motor ODE for the given inputs / The motors ODE-System.

Overriding this method is optional for each subclass. If it is overridden, the parameter HAS_JACOBIAN must also be set to True. Otherwise, the jacobian will not be called.

Parameters:

  • state (ndarray(float)) – The motors state.

  • u_in (list(float)) – The motors input voltages.

  • omega (float) – Angular velocity of the motor

Returns:

[0]: Derivatives of all electrical motor states over all electrical motor states shape:(states x states) [1]: Derivatives of all electrical motor states over omega shape:(states,) [2]: Derivative of Torque over all motor states shape:(states,)

Return type:

Tuple(ndarray, ndarray, ndarray)

Permanent Magnet Synchronous Motor

The PMSM is a three phase motor with a permanent magnet in the rotor as shown in the figure [Boecker2018b]. The input of this motor are the voltages \(u_a\), \(u_b\) and \(u_c\).

The quantities are:

  • \(u_a\), \(u_b\), \(u_c\) phase voltages

  • \(i_a\), \(i_b\), \(i_c\) phase currents

  • \(R_s\) stator resistance

  • \(L_d\) d-axis inductance

  • \(L_q\) q-axis inductance

  • \(i_{sd}\) d-axis current

  • \(i_{sq}\) q-axis current

  • \(u_{sd}\) d-axis voltage

  • \(u_{sq}\) q-axis voltage

  • \(p\) pole pair number

  • \(\mathit{\Psi}_p\) permanent linked rotor flux

  • \(\epsilon\) rotor position angle

  • \(\omega\) (electrical) angular velocity

  • \(\omega_{me}\) mechanical angular velocity

  • \(T\) Torque produced by the motor

  • \(T_L\) Torque from the load

  • \(J\) moment of inertia

The electrical angular velocity and the mechanical angular velocity are related such that \(\omega=\omega_{me} p\).

../../_images/GDAFig29.svg

The circuit diagram of the phases are similar to each other and the armature circuit of the externally excited motor.

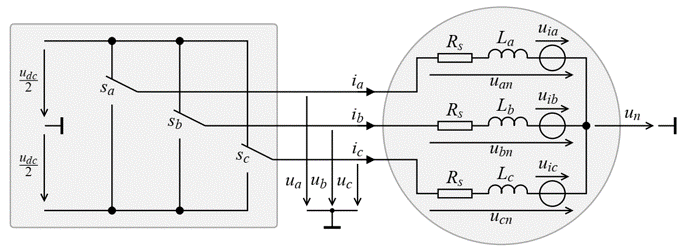
../../_images/pmsmMotorB6.png

For an easy computation the three phases are first transformed to the quantities \(\alpha\) and \(\beta\) and afterwards to \(d/q\) coordinates that rotated with the rotor as given in [Boecker2018b].

../../_images/ESBdq.svg

This results in the equations:

\(u_{sd}=R_s i_{sd}+L_d \frac{\mathrm{d} i_{sd}}{\mathrm{d} t}-\omega_{me}p L_q i_{sq}\)

\(u_{sq}=R_s i_{sq}+L_q \frac{\mathrm{d} i_{sq}}{\mathrm{d} t}+\omega_{me}p L_d i_{sd}+\omega_{me}p \mathit{\Psi}_p\)

\(\frac{\mathrm{d} \omega_{me}}{\mathrm{d} t}=\frac{T-T_L(\omega_{me})}{J}\)

\(T=\frac{3}{2} p (\mathit{\Psi}_p +(L_d-L_q)i_{sd}) i_{sq}\)

A more detailed derivation can be found in [Modeling and High-Performance Control of Electric Machines, John Chiasson (2005)]

The difference between rms and peak values and between line and phase quantities has to be considered at the PMSM. The PMSM is in star conncetion and the line voltage \(U_L\) is mostly given in data sheets as rms value. In the toolbox the nominal value of the phase voltage \(\hat{U}_S=\sqrt{\frac{2}{3}}U_L\) is needed. Furthermore, the supply voltage is typically the same \(u_{sup}=\hat{U}_S\). For example, a line voltage of \(U_L=400~\text{V}\) is given, the rms phase voltage is \(U_S=\sqrt{\frac{1}{3}}U_L = 230.9 \text{ V}\) and the peak value \(\hat{U}_S=326.6 \text{ V}\). The nominal peak current of a phase is given by \(\hat{I}_S=\sqrt{2} I_S\).

../../_images/Drehstromtrafo.svg
class gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor(motor_parameter=None, nominal_values=None, limit_values=None, motor_initializer=None)[source]

Motor Parameter

Unit

Default Value

Description

r_s

Ohm

18e-3

Stator resistance

l_d

H

0.37e-3

Direct axis inductance

l_q

H

1.2e-3

Quadrature axis inductance

p

1

3

Pole pair number

j_rotor

kg/m^2

0.03883

Moment of inertia of the rotor

Motor Currents

Unit

Description

i_sd

A

Direct axis current

i_sq

A

Quadrature axis current

i_a

A

Current through line a

i_b

A

Current through line b

i_c

A

Current through line c

i_alpha

A

Current in alpha axis

i_beta

A

Current in beta axis

Motor Voltages

Unit

Description

u_sd

V

Direct axis voltage

u_sq

V

Quadrature axis voltage

u_a

V

Phase voltage for line a

u_b

V

Phase voltage for line b

u_c

V

Phase voltage for line c

u_alpha

V

Phase voltage in alpha axis

u_beta

V

Phase voltage in beta axis

Limits /

Nominal Value Dictionary Entries:

Entry

Description

i

General current limit / nominal value

i_a

Current in phase a

i_b

Current in phase b

i_c

Current in phase c

i_alpha

Current in alpha axis

i_beta

Current in beta axis

i_sd

Current in direct axis

i_sq

Current in quadrature axis

omega

Mechanical angular Velocity

torque

Motor generated torque

epsilon

Electrical rotational angle

u_a

Phase voltage in phase a

u_b

Phase voltage in phase b

u_c

Phase voltage in phase c

u_alpha

Phase voltage in alpha axis

u_beta

Phase voltage in beta axis

u_sd

Phase voltage in direct axis

u_sq

Phase voltage in quadrature axis

Note

The voltage limits should be the peak-to-peak value of the phase voltage (\(\hat{u}_S\)). A phase voltage denotes the potential difference from a line to the neutral point in contrast to the line voltage between two lines. Typically the RMS value for the line voltage (\(U_L\)) is given as \(\hat{u}_S=\sqrt{2/3}~U_L\)

The current limits should be the peak-to-peak value of the phase current (\(\hat{i}_S\)). Typically the RMS value for the phase current (\(I_S\)) is given as \(\hat{i}_S = \sqrt{2}~I_S\)

If not specified, nominal values are equal to their corresponding limit values. Furthermore, if specific limits/nominal values (e.g. i_a) are not specified they are inferred from the general limits/nominal values (e.g. i)

Parameters:

  • motor_parameter – Motor parameter dictionary. Contents specified for each motor.

  • nominal_values – Nominal values for the motor quantities.

  • limit_values – Limits for the motor quantities.

  • motor_initializer –

    Initial motor states (currents) (‘constant’, ‘uniform’, ‘gaussian’ sampled from

    given interval or out of nominal motor values)

  • initial_limits – limits for of the initial state-value

HAS_JACOBIAN = True

Parameter indicating if the class is implementing the optional jacobian function

electrical_jacobian(state, u_in, omega, *args)[source]

Calculation of the jacobian of each motor ODE for the given inputs / The motors ODE-System.

Overriding this method is optional for each subclass. If it is overridden, the parameter HAS_JACOBIAN must also be set to True. Otherwise, the jacobian will not be called.

Parameters:

  • state (ndarray(float)) – The motors state.

  • u_in (list(float)) – The motors input voltages.

  • omega (float) – Angular velocity of the motor

Returns:

[0]: Derivatives of all electrical motor states over all electrical motor states shape:(states x states) [1]: Derivatives of all electrical motor states over omega shape:(states,) [2]: Derivative of Torque over all motor states shape:(states,)

Return type:

Tuple(ndarray, ndarray, ndarray)

References

[Boecker2018a]

Böcker, Joachim; Elektrische Antriebstechnik; 2018; Paderborn University

[Boecker2018b] (1,2)

Böcker, Joachim; Controlled Three-Phase Drives; 2018; Paderborn University

[Chiasson2005]

Chiasson, John; Modeling and High-Performance Control of Electric Machines; 2005; Hoboken, NJ, USA