Finite-Control-Set Model Predictive Control (FCS-MPC)

We apply a finite-control set (FCS) model predictive control (MPC) approach to realize current control of a permanent magnet synchronous motor (PMSM) and Synchronous Reluctance Motor (SRM) in rotor field-oriented coordinates. Unlike continuous-control set (CCS) MPC, FCS-MPC directly evaluates a finite set of switching states to optimize the control input based on a cost function over a prediction horizon.

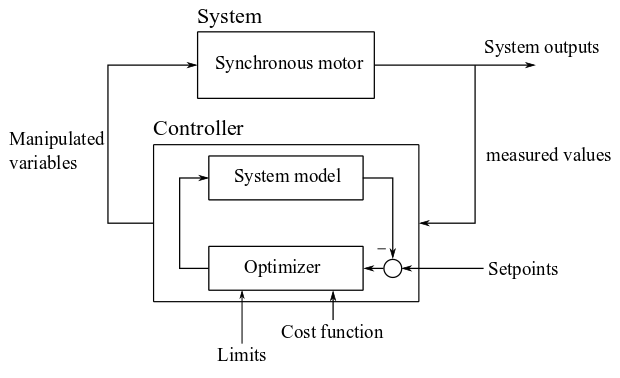
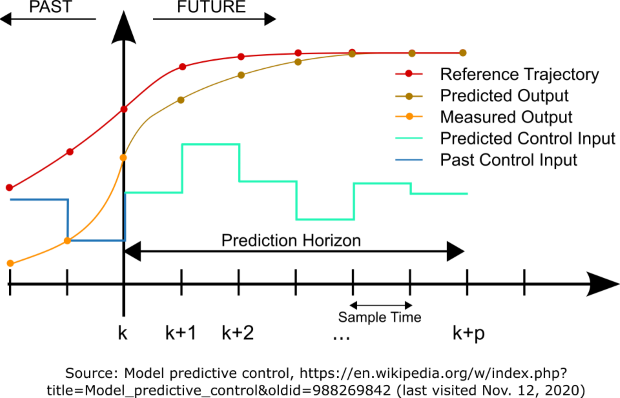
With the help of the system model, the output variables are predicted for each possible switching state in the finite control set. The optimizer evaluates a cost function (typically the quadratic control error) for all possible switching combinations over the prediction horizon. The switching state that minimizes the cost function is selected and applied to the system in the next time step.

Unlike CCS-MPC, FCS-MPC does not require an iterative numerical solver or barrier functions to handle constraints, as the voltage limits are inherently respected by evaluating only the physically realizable switching states of the converter. The computational efficiency of FCS-MPC comes from the direct enumeration and evaluation of the finite number of possible switching states, rather than solving an optimization problem with constraints.

MPC Current Controller

class gem_controllers.mpc_current_controller.MPCCurrentController(env, env_id, prediction_horizon=1, w_d=1.0, w_q=1.0)

Bases: GemController

Parameters:

• env – Gym environment instance

• env_id – Environment ID string

• prediction_horizon – Prediction horizon (N)

• w_d – Weight for d-axis current error

• w_q – Weight for q-axis current error

control(state, reference)

Calculate the voltage reference.

Parameters:

• state (np.array) – state of the environment

• reference (np.array) – speed references

Returns:

reference voltage

Return type:

np.array

control_environment(env, n_steps, max_episode_length=inf, render_env=False)

Function to control an environment with the GemController.

Parameters:

• env (ElectricMotorEnvironment) – The GEM-Environment that the controller should control.

• n_steps (int) – Number of iteration steps.

• max_episode_length (int) – Maximum length of an epsiode, after which the environment and controller should be reset.

• render_env (bool) – Flag, if the states of the environment should be plotted.

get_signal_value(signal_name)

Get the value of a signal calling by the signal name.

Parameters:

signal_name (str) – Name of a signal of the state

Returns:

float

classmethod make(env: ~gym_electric_motor.core.ElectricMotorEnvironment, env_id: str, decoupling: bool = True, current_safety_margin: float = 0.2, base_current_controller: str = 'PI', base_speed_controller: str = 'PI', a: int = 4, should_plot: bool = False, plot_references: bool = True, block_diagram: bool = True, save_block_diagram_as: (<class 'str'>, <class 'tuple'>) = None, **kwargs)

A factory function that generates (and parameterizes) a matching GemController for a given gym-electric-motor environment env.

Parameters:

• env (ElectricMotorEnvironment) – The GEM-Environment that the controller shall be created for.

• env_id (str) – The corresponding environment-id to specify the concrete environment.

• decoupling (bool) – Flag, if a EMF-Feedforward correction stage should be used in the pi current controller.

• current_safety_margin (float in [0..1]) – The ratio between the maximum current set point the reference controller generates and the absolute current limit.

• base_speed_controller ('PI'/'PID'/'P'/'ThreePoint') – Selection of the basic control algorithm for the speed controller.

• base_current_controller ('PI'/'PID'/'P'/'ThreePoint') – Selection of the basic control algorithm for the current controller.

• a (float) – Tuning parameter of the symmetrical optimum.

• plot_references (bool) – Flag, if the reference values of the underlying control circuits should be plotted

• block_diagram (bool) – Selection whether the block diagram should be displayed

• save_block_diagram_as (str, tuple) – Selection of whether the block diagram should be saved

Returns:

An initialized (and tuned) instance of a controller that fits to the specified environment.

Return type:

GemController

reset()

Reset all stages of the controller

tune(env, env_id, **kwargs)

property signal_names

Signal names of the controller

property signals

Input signals of the controller

property stages

Stages of the GEM Controller

u_abc_k1

Load motor model constants and motor-specific state names

u_lim

Setup coordinate transforms and precompute voltage combinations

w_q

Assign self.step from the environment wrapper, default to 0 if no DeadTimeProcessor

Example Usage

The following example demonstrates how to apply the MPCCurrentController to control a permanent magnet synchronous motor (PMSM) using a finite-control-set MPC approach within the gym-electric-motor simulation environment.

import numpy as np
import matplotlib
matplotlib.use('Qt5Agg')
from gem_controllers import GemController
import gym_electric_motor as gem
from gym_electric_motor.envs.motors import ActionType, ControlType, Motor, MotorType
from gym_electric_motor.physical_systems import ConstantSpeedLoad
from gym_electric_motor.reference_generators import (
    MultipleReferenceGenerator, SwitchedReferenceGenerator,
    TriangularReferenceGenerator, SinusoidalReferenceGenerator,
    StepReferenceGenerator
)
from gym_electric_motor.visualization.motor_dashboard import MotorDashboard

motor_parameter = dict(r_s=15e-3, l_d=0.37e-3, l_q=1.2e-3, psi_p=65.6e-3, p=3, j_rotor=0.06)
limit_values = dict(i=160 * 1.41, omega=12000 * np.pi / 30, u=450)
nominal_values = {key: 0.7 * limit for key, limit in limit_values.items()}

q_generator = SwitchedReferenceGenerator(
    sub_generators=[
        SinusoidalReferenceGenerator(reference_state='i_sq', amplitude_range=(0, 0.3), offset_range=(0, 0.2)),
        StepReferenceGenerator(reference_state='i_sq', amplitude_range=(0, 0.5)),
        TriangularReferenceGenerator(reference_state='i_sq', amplitude_range=(0, 0.3), offset_range=(0, 0.2))
    ],
    super_episode_length=(500, 1000)
)

d_generator = SwitchedReferenceGenerator(
    sub_generators=[
        SinusoidalReferenceGenerator(reference_state='i_sd', amplitude_range=(0, 0.3), offset_range=(0, 0.2)),
        StepReferenceGenerator(reference_state='i_sd', amplitude_range=(0, 0.5)),
        TriangularReferenceGenerator(reference_state='i_sd', amplitude_range=(0, 0.3), offset_range=(0, 0.2))
    ],
    super_episode_length=(500, 1000)
)

reference_generator = MultipleReferenceGenerator([d_generator, q_generator])

visu = MotorDashboard(state_plots=['i_sq', 'i_sd', 'u_sq', 'u_sd'], update_interval=10)

motor = Motor(
    MotorType.PermanentMagnetSynchronousMotor,
    ControlType.CurrentControl,
    ActionType.Finite
)

env = gem.make(
    motor.env_id(),
    visualization=visu,
    load=ConstantSpeedLoad(omega_fixed=1000 * np.pi / 30),
    reference_generator=reference_generator,
    reward_function=dict(
        reward_weights={'i_sq': 1, 'i_sd': 1},
        reward_power=0.5,
    ),
    supply=dict(u_nominal=400),
    motor=dict(
        motor_parameter=motor_parameter,
        limit_values=limit_values,
        nominal_values=nominal_values
    ),
)

visu.initialize()

controller = GemController.make(
    env=env,
    env_id=motor.env_id(),
    base_current_controller="MPC",
    block_diagram=False,
    prediction_horizon=1,
    w_d=0.5,
    w_q=2.0
)

(state, reference), _ = env.reset()
cum_rew = 0

for i in range(10000):
    env.render()
    action = controller.control(state, reference)
    (state, reference), reward, terminated, truncated, _ = env.step(action)
    cum_rew += reward
    if terminated:
        (state, reference), _ = env.reset()
        controller.reset()

print('Reward =', cum_rew)
env.close()

Simulation Results

The following figures illustrate the performance of the FCS-MPC controller in current control of the PMSM under varying reference trajectories. The controller accurately tracks both the d- and q-axis current references while ensuring smooth control actions.

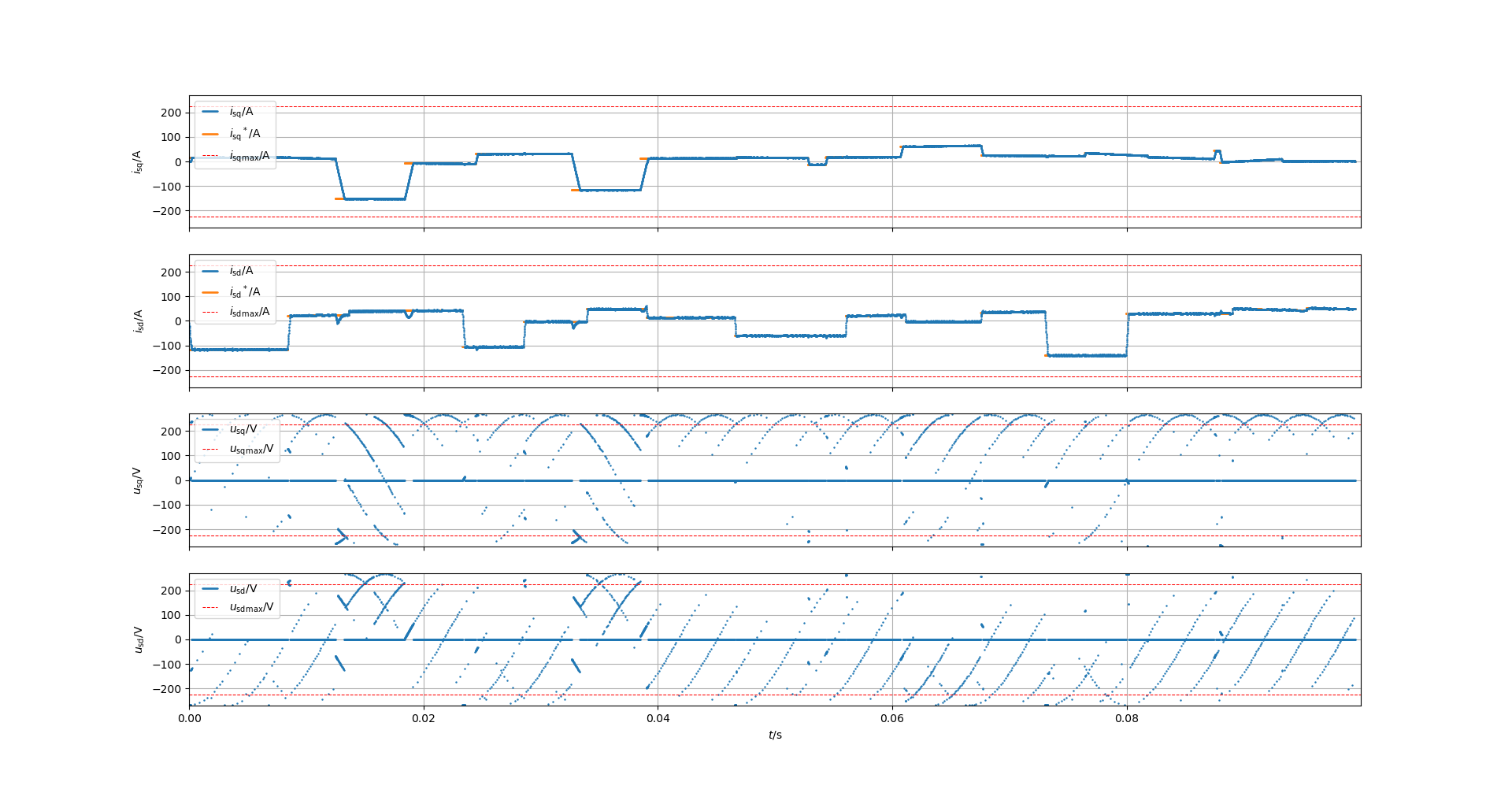
FCS-MPC current tracking of i_d and i_q.

The results show that the finite-control-set MPC effectively minimizes the current tracking error within each sampling period while satisfying the converter switching constraints. Compared to conventional PI controllers, the FCS-MPC achieves faster dynamic response and improved steady-state performance without overshoot.