Electric Motors

Electric Motor Base Class

class gym_electric_motor.physical_systems.electric_motors.ElectricMotor(motor_parameter=None, nominal_values=None, limit_values=None, motor_initializer=None, initial_limits=None)

Bases: RandomComponent

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

electrical_jacobian(state, u_in, omega, *_)

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.electrical_jacobian.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

electrical_ode(state, u_in, omega, *_)

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.electrical_ode.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

i_in(state)

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.i_in.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

initialize(state_space, state_positions, **__)

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.initialize.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

next_generator()

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.next_generator.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

reset(state_space, state_positions, **__)

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.reset.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

seed(seed=None)

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.seed.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

CURRENTS = []

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.CURRENTS.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

CURRENTS_IDX = []

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.CURRENTS_IDX.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

HAS_JACOBIAN = False

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.HAS_JACOBIAN.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

VOLTAGES = []

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.VOLTAGES.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property initial_limits

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.initial_limits.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property initializer

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.initializer.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property limits

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.limits.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property motor_parameter

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.motor_parameter.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property nominal_values

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.nominal_values.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property random_generator

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.random_generator.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property seed_sequence

API for gym_electric_motor.physical_systems.electric_motors.ElectricMotor.seed_sequence.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

Synchronous Motors

Parameter Dictionary

Key	Description	Default
r_s	Stator Resistance in Ohm	4.9
l_d	d-axis inductance in Henry	79e-3
l_q	q-axis inductance in Henry	113e-3
j_rotor	Moment of inertia of the rotor	2.45e-3
psi_p	Permanent linked rotor flux	0.165
p	Pole pair Number	2

All nominal voltages and currents are peak phase values. Therefore, data sheet values for line voltages and phase currents has to be transformed such that \(U_N=\sqrt(2/3) U_L\) and \(I_N=\sqrt(2) I_S\).

Furthermore, the angular velocity is the electrical one and not the mechanical one \(\omega = p \omega_{me}\).

class gym_electric_motor.physical_systems.electric_motors.SynchronousMotor(motor_parameter=None, nominal_values=None, limit_values=None, motor_initializer=None)

Bases: ThreePhaseMotor

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

electrical_jacobian(state, u_in, omega, *_)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.electrical_jacobian.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

electrical_ode(state, u_dq, omega, *_)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.electrical_ode.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

i_in(state)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.i_in.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

initialize(state_space, state_positions, **__)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.initialize.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

next_generator()

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.next_generator.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

static q(quantities, epsilon)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.q.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

static q_inv(quantities, epsilon)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.q_inv.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

q_inv_me(quantities, epsilon)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.q_inv_me.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

q_me(quantities, epsilon)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.q_me.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

reset(state_space, state_positions, **__)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.reset.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

seed(seed=None)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.seed.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

static t_23(quantities)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.t_23.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

static t_32(quantities)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.t_32.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

torque(state)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.torque.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

CURRENTS = ['i_sd', 'i_sq']

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.CURRENTS.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

CURRENTS_IDX = [0, 1]

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.CURRENTS_IDX.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

EPSILON_IDX = 2

HAS_JACOBIAN = False

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.HAS_JACOBIAN.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

I_SD_IDX = 0

I_SQ_IDX = 1

VOLTAGES = ['u_sd', 'u_sq']

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.VOLTAGES.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property initial_limits

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.initial_limits.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property initializer

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.initializer.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property limits

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.limits.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property motor_parameter

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.motor_parameter.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property nominal_values

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.nominal_values.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property random_generator

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.random_generator.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property seed_sequence

API for gym_electric_motor.physical_systems.electric_motors.SynchronousMotor.seed_sequence.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

Synchronous Reluctance Motor

class gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor(motor_parameter=None, nominal_values=None, limit_values=None, motor_initializer=None)

Bases: SynchronousMotor

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

electrical_jacobian(state, u_in, omega, *_)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.electrical_jacobian.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

electrical_ode(state, u_dq, omega, *_)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.electrical_ode.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

i_in(state)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.i_in.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

initialize(state_space, state_positions, **__)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.initialize.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

next_generator()

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.next_generator.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

static q(quantities, epsilon)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.q.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

static q_inv(quantities, epsilon)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.q_inv.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

q_inv_me(quantities, epsilon)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.q_inv_me.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

q_me(quantities, epsilon)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.q_me.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

reset(state_space, state_positions, **__)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.reset.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

seed(seed=None)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.seed.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

static t_23(quantities)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.t_23.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

static t_32(quantities)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.t_32.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

torque(currents)

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.torque.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

CURRENTS = ['i_sd', 'i_sq']

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.CURRENTS.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

CURRENTS_IDX = [0, 1]

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.CURRENTS_IDX.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

EPSILON_IDX = 2

HAS_JACOBIAN = True

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.HAS_JACOBIAN.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

IO_CURRENTS = ['i_a', 'i_b', 'i_c', 'i_sd', 'i_sq']

IO_VOLTAGES = ['u_a', 'u_b', 'u_c', 'u_sd', 'u_sq']

I_SD_IDX = 0

I_SQ_IDX = 1

VOLTAGES = ['u_sd', 'u_sq']

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.VOLTAGES.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property initial_limits

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.initial_limits.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property initializer

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.initializer.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property limits

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.limits.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property motor_parameter

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.motor_parameter.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property nominal_values

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.nominal_values.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property random_generator

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.random_generator.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property seed_sequence

API for gym_electric_motor.physical_systems.electric_motors.SynchronousReluctanceMotor.seed_sequence.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

Permanent Magnet Synchronous Motor

The PMSM is a three phase motor with a permanent magnet in the rotor as shown in the figure [Boecker2018b]. The input of this motor are the voltages \(u_a\), \(u_b\) and \(u_c\).

The quantities are:

• \(u_a\), \(u_b\), \(u_c\) phase voltages

• \(i_a\), \(i_b\), \(i_c\) phase currents

• \(R_s\) stator resistance

• \(L_d\) d-axis inductance

• \(L_q\) q-axis inductance

• \(i_{sd}\) d-axis current

• \(i_{sq}\) q-axis current

• \(u_{sd}\) d-axis voltage

• \(u_{sq}\) q-axis voltage

• \(p\) pole pair number

• \(\mathit{\Psi}_p\) permanent linked rotor flux

• \(\epsilon\) rotor position angle

• \(\omega\) (electrical) angular velocity

• \(\omega_{me}\) mechanical angular velocity

• \(T\) Torque produced by the motor

• \(T_L\) Torque from the load

• \(J\) moment of inertia

The electrical angular velocity and the mechanical angular velocity are related such that \(\omega=\omega_{me} p\).

The circuit diagram of the phases are similar to each other and the armature circuit of the externally excited motor.

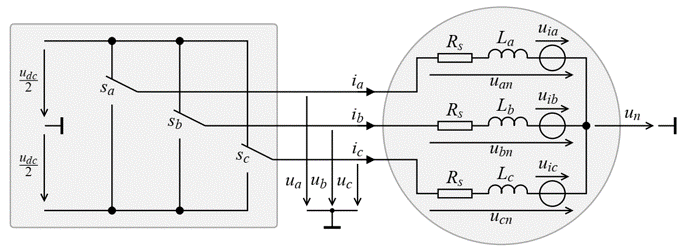
For an easy computation the three phases are first transformed to the quantities \(\alpha\) and \(\beta\) and afterwards to \(d/q\) coordinates that rotated with the rotor as given in [Boecker2018b].

This results in the equations:

\(u_{sd}=R_s i_{sd}+L_d \frac{\mathrm{d} i_{sd}}{\mathrm{d} t}-\omega_{me}p L_q i_{sq}\)

\(u_{sq}=R_s i_{sq}+L_q \frac{\mathrm{d} i_{sq}}{\mathrm{d} t}+\omega_{me}p L_d i_{sd}+\omega_{me}p \mathit{\Psi}_p\)

\(\frac{\mathrm{d} \omega_{me}}{\mathrm{d} t}=\frac{T-T_L(\omega_{me})}{J}\)

\(T=\frac{3}{2} p (\mathit{\Psi}_p +(L_d-L_q)i_{sd}) i_{sq}\)

A more detailed derivation can be found in [Modeling and High-Performance Control of Electric Machines, John Chiasson (2005)]

The difference between rms and peak values and between line and phase quantities has to be considered at the PMSM. The PMSM is in star conncetion and the line voltage \(U_L\) is mostly given in data sheets as rms value. In the toolbox the nominal value of the phase voltage \(\hat{U}_S=\sqrt{\frac{2}{3}}U_L\) is needed. Furthermore, the supply voltage is typically the same \(u_{sup}=\hat{U}_S\). For example, a line voltage of \(U_L=400~\text{V}\) is given, the rms phase voltage is \(U_S=\sqrt{\frac{1}{3}}U_L = 230.9 \text{ V}\) and the peak value \(\hat{U}_S=326.6 \text{ V}\). The nominal peak current of a phase is given by \(\hat{I}_S=\sqrt{2} I_S\).

class gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor(motor_parameter=None, nominal_values=None, limit_values=None, motor_initializer=None)

Bases: SynchronousMotor

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

electrical_jacobian(state, u_in, omega, *args)

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.electrical_jacobian.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

electrical_ode(state, u_dq, omega, *_)

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.electrical_ode.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

i_in(state)

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.i_in.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

initialize(state_space, state_positions, **__)

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.initialize.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

next_generator()

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.next_generator.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

static q(quantities, epsilon)

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.q.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

static q_inv(quantities, epsilon)

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.q_inv.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

q_inv_me(quantities, epsilon)

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.q_inv_me.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

q_me(quantities, epsilon)

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.q_me.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

reset(state_space, state_positions, **__)

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.reset.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

seed(seed=None)

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.seed.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

static t_23(quantities)

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.t_23.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

static t_32(quantities)

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.t_32.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

torque(currents)

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.torque.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

CURRENTS = ['i_sd', 'i_sq']

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.CURRENTS.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

CURRENTS_IDX = [0, 1]

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.CURRENTS_IDX.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

EPSILON_IDX = 2

HAS_JACOBIAN = True

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.HAS_JACOBIAN.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

IO_CURRENTS = ['i_a', 'i_b', 'i_c', 'i_sd', 'i_sq']

IO_VOLTAGES = ['u_a', 'u_b', 'u_c', 'u_sd', 'u_sq']

I_SD_IDX = 0

I_SQ_IDX = 1

VOLTAGES = ['u_sd', 'u_sq']

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.VOLTAGES.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property initial_limits

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.initial_limits.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property initializer

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.initializer.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property limits

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.limits.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property motor_parameter

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.motor_parameter.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property nominal_values

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.nominal_values.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property random_generator

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.random_generator.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

property seed_sequence

API for gym_electric_motor.physical_systems.electric_motors.PermanentMagnetSynchronousMotor.seed_sequence.

Note

The original docstring is temporarily suppressed due to formatting issues upstream. Once it’s cleaned, we’ll restore the full text here.

References

[Boecker2018a]

Böcker, Joachim; Elektrische Antriebstechnik; 2018; Paderborn University

[Boecker2018b] (1,2)

Böcker, Joachim; Controlled Three-Phase Drives; 2018; Paderborn University

[Chiasson2005]

Chiasson, John; Modeling and High-Performance Control of Electric Machines; 2005; Hoboken, NJ, USA